Seeing High School Math In a New Ways!

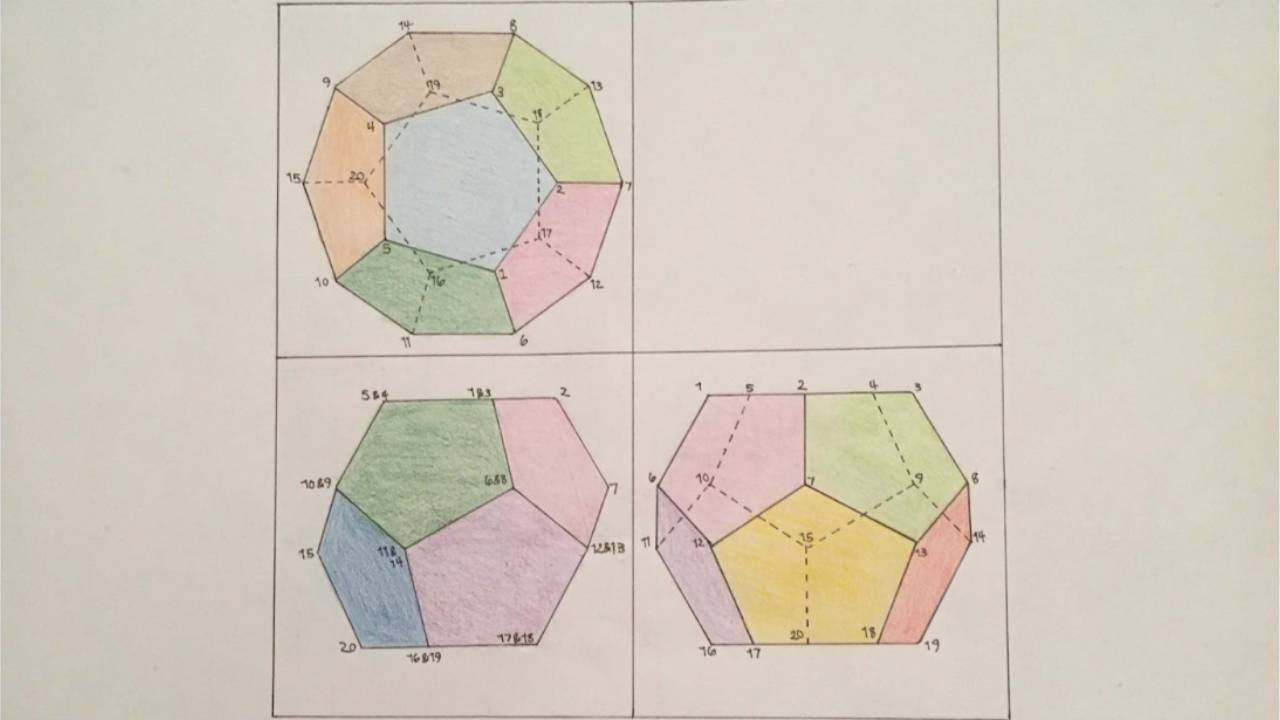
Math is often seen as a skill that everyone must learn as part of a well rounded education, and this is true to a point.  However, if that was the sum total of what was taught in math, it could be a very dry and torturous experience indeed!  The real value of math in the 9th and 10th grade curricula at Seasons of Seven is to be able to think about the world in new ways, and from different perspectives, sometimes literally!

In the 9th grade Descriptive Geometry Main Lesson, students learn to move their perspective around a three dimensional object.  This starts by imagining a stick in a box.  If we imagine viewing the stick from the front of the box, we have one view.  What does that view tell us about what the stick will look like from the top? From the side?  From there, we can do a similar exercise with a triangle.  How can something look like an equilateral triangle from the front, a scalene triangle from the top, and a straight line from the side?  Then we move on to a three dimensional object - a pyramid with a pentagonal base.  Finally, we can put the information we have gathered together to make a three perspective drawing of a Platonic Solid - the dodecahedron.

Students must consider what parts of the dodecahedron are distorted in the top, front and side views, and which are actual size.  This has implications for how we construct those views.  The final task is to be able to identify what parts of the dodecahedron we are looking at in the various views.

Students learn to free themselves from their preconceptions of what they think they will see, and meet the object on its terms.  This has important implications for the development of flexible thinking, which is not just significant in mathematics, but carries over into all other aspects of life - everything from trying new food to objectively listening to an opinion that is different from your own.

This process continues in 10th Grade Geometry, where students confront the lawfulness of math. This has its clearest expression in geometric proof.  If A is true and B is true, C must be true (eg., if the sides of a square are equal, and the given figure is a square, its sides must be equal.)  This also expresses itself in geometric construction.  If we construct a triangle inscribed in a circle, and choose a random point on the circle, we can construct three perpendicular lines from that point to the sides of the triangle. The three points where those perpendiculars intersect the sides of the triangle are themselves on a line.  If we repeat this seemingly random process for as many points on the circle as we can, a new figure emerges - the hypocycloid.  This happens with ANY triangle inscribed in a circle.  How can such a banal process produce a completely new figure?  This kind of experience challenges students to consider the wider implications of seemingly simple mathematics.  The world becomes a little more mysterious, and a little more interesting and worth exploring!

We are Redefining Education!
We invite you to join us every Monday for our Q and A.
We are here to support you in living your family’s best life!

Learn more about high school HERE.